Answer:
The equation of the line perpendicular to the given line is
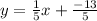 .
.
The equation of the line perpendicular to the given line is
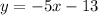 .
.
Explanation:
The given line is y=-5x+6
The slope of the given line,
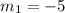
Let
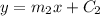 be the slope of the line perpendicular to y=-5x+6,
be the slope of the line perpendicular to y=-5x+6,
where
 is constant.
is constant.
As multiplication of slopes of two perpendicular lines equal to -1, so
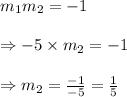
So, the equation of the line perpendicular to the given line is
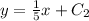 which passes through the point (-2,-3), so
which passes through the point (-2,-3), so
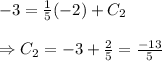
Hence, the equation of the line perpendicular to the given line is
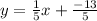 .
.
Now, let
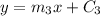 be the equation of the parallel line to y=-5x+6.
be the equation of the parallel line to y=-5x+6.
As the slopes of two parallel lines are the same, so
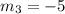 .
.
So, the equation of the parallel line becomes
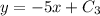 which passes through the point (-2,-3), so
which passes through the point (-2,-3), so
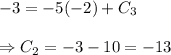
Hence, the equation of the line perpendicular to the given line is
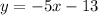 .
.