Question

3. Two balls are rolling toward each other. One has a momentum of 85kg*m/s, and the other has a momentum of -85kg*m/s. What will be the total momentum of the system after they collide? In what direction will they move after they collide if it is an inelastic collision? Answer:​

Answer 1

The total momentum is zero.

Step-by-step explanation:

This problem can be solved by applying the momentum conservation theorem and the amount of motion. This theorem tells us that the amount of motion is conserved before and after a collision.

In the next equation, we will write to the left of the equal sign the amount of motion before the collision and to the right the amount of motion after the collision.

`(P_(1))-(P_(2))=P_(3)`

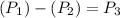
where:

P₁ = momentum of the ball moving to the right, before the collision = 85 [kg*m/s]

P₂ = momentum of the ball moving to the left, before the collision = - 85 [kg*m/s]

P₃ = Final momentum after the collision [kg*m/s]

`(85) - 85 = P_(3)\\P_(3)= 0`

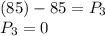
There is no movement of any of the balls, they remain at rest after the impact.