Question

(5) A 4 kg. object rests on a flat, horizontal surface with a static

coefficient of friction of 0.25. What minimum force will be necessary to
start the object in motion? If the coefficient was smaller, what effect would
that have? If it was larger?

Answer 1

F = 9.81 [N]

Step-by-step explanation:

To solve this problem we must use Newton's third le which tells us that the sum of forces on a body that remains static must be equal to one resulting from these forces in the opposite direction.

Let's perform a summation of forces on the vertical axis-y to determine the normal force N.

∑F = 0 (axis-y)

`N - m*g = 0`

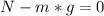
where:

m = mass = 4 [kg]

g = gravity acceleration = 9.81 [m/s²]

`N - (4*9.81)=0\\N = 39.24 [N]`

Now we know that the frictional force can be calculated using the following equation.

f = μ*N

where:

f = friction force [N]

μ = friction coefficient = 0.25

N = normal force = 39.24 [N]

Now replacing:

`f = 0.25*39.24\\f = 9.81[N]`

Then we perform a sum of forces on the X-axis equal to zero. This sum of forces allows us to determine the minimum force to be able to move the object in a horizontal direction.

∑F = 0 (axis-x)

`F-f=0\\F-9.81=0\\F= 9.81[N]`

If the coefficient was smaller, a smaller force (F) would be needed to start the movement, this can be easily seen by replacing the value of 0.25, by smaller values, such as 0.1 or 0.05.

If the coefficient were larger, a larger force would be needed.