Question

1. If the coefficient of static friction is,μ=.72 for the surface which the man is standing on, then what is the force of friction. Ff=μFn

2. If the velocity of the car below has an initial velocity of 5m/s and is projected at an angle of 60 degrees relative to the horizontal then what is the total time of travel, the range and maximum height?
3.A cyclist is riding with an initial velocity of 16m/s when she notices a cat in front of her. She then slows down and begins coasting with a constant acceleration of -.62m/s2. Find the time it will take the cyclist to stop.
The main kinematic equations,
Vf=Vo+at
(Vf)2=(Vo)2+2aΔx
Δx=Vot+(½)at2
4.A ball with a mass of 5kg is dropped from a height of 20m. How long will it take the ball to reach the ground.


HELP ASAP

Answer 1

1. The force of friction
`F_f =0.72 * F_n`

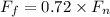
2. The total travel time is approximately 0.884 seconds

The range is approximately 2.209 m

The maximum height reached is approximately 0.383 m

3. The time it will take the cyclist to stop is approximately 25.806 seconds

4. The time it will take the ball to reach the ground is approximately 2.020 seconds

Step-by-step explanation:

1. Given that the coefficient of static friction, μ = 0.72, we have;

`F_f = \mu \cdot F_n = 0.72 * F_n`

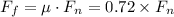
2. The given parameters are;

The initial velocity of the car, v = 5 m/s

The direction of the vehicle = 60° to the horizontal

Therefore, we have;

The vertical component of the velocity,
`v_y` = 5 × sin(60°) = 2.5×√3

`v_y` = 2.5×√3 m/s

The total travel time, t = 2·u·sin(θ)/g = 2 × 5 × sin(60°)/9.8 ≈ 0.884

The total travel time, t ≈ 0.884 seconds

The range, R = (u²·sin(2·θ))/g = 5² × sin(120°)/9.8 ≈ 2.209

The maximum height is given from the v² =
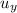`u_y`² - 2·g·h

Where;

v = The final velocity = 0 m/s at maximum height

h =
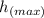`h_((max))` = The maximum height

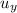`u_y` = The initial vertical velocity = 2.5·√3

∴ 0² = 2.5·√3² - 2 × 9.8 ×
`h_((max))`

2.5·√3² = 2 × 9.8 ×
`h_((max))`

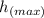
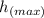
`h_((max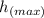))` = 2.5·√3²/(2 × 9.8) ≈ 0.383

The maximum height =
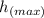`h_((max))` = 0.383 m

3. The given parameters are;

The initial velocity of the cyclist, v₀ = 16 m/s

The deceleration of the cyclist, a = -0.62 m/s²

At the point the cyclist stops, the final velocity,
`v_f` = 0

Therefore, from the given kinematic equations, we have;

`v_f` = v₀ + a·t

Where t, is the time it will take the cyclist to stop

∴ t = (
`v_f` - v₀)/a = (0 - 16)/(-0.62) ≈ 25.806

Therefore, the time it will take the cyclist to stop = t ≈ 25.806 seconds

4. The time, t, it will take the ball to reach the ground, from a height, h = 20 meters is given by the equation of free fall as follows;

h = 1/2·g·t²

Where;

g = The acceleration due to gravity = 9.8 m/s²

Therefore, we have;

t² = h/(1/2·g)

t = √(h/(1/2·g)) = √(20/(1/2 × 9.8)) = 2.0203050891 ≈ 2.02

The time it will take the ball to reach the ground, t ≈ 2.020 seconds.