Given:
Focus of a parabola = (0,2)
Directrix: y=0.
To find:
The equation of parabola.
Solution:
The equation of parabola is
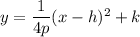 ...(i)
...(i)
where, (h,k) is vertex, (h,k+p) is focus, y=k-p is directrix.
Focus :

On comparing both sides, we get
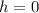
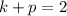 ...(ii)
...(ii)
On comparing y=k-p and y=0, we get
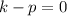 ...(iii)
...(iii)
Adding (ii) and (iii), we get
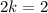
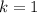
Putting k=1 in (ii).
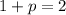
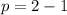
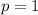
Putting h=0, k=1 and p=1 in (i).
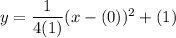
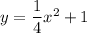
Therefore, the equation of required parabola is
 .
.