Given:
The function is
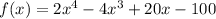
To find:
The remainder if f(x) is divided by (x+11).
Solution:
According to the remainder theorem, if a function f(x) is divided by (x-c), then the remainder is f(c).
On comparing (x+11) and (x-c), we get c=-11.
Using remainder theorem, if a function f(x) is divided by (x+11), then the remainder is f(-11).
Putting x=-11 in the given function.
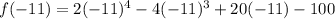
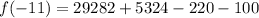
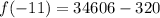
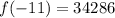
Therefore, the remainder is 34286 when f(x) is divided by (x+11).