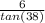Answer:
The statement would best represent the value of a is a =
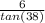 ⇒ c
⇒ c
Explanation:
In the right angle triangle, we can use the trigonometry ratios to find the missing sides or angles
- sin β =
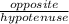
- cos β =
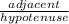
- tan β =
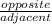
In the given right triangle
∵ There measure of an acute angle is 38°
∵ The adjacent side to this angle is a
∵ The opposite side to this angle is 6
→ We will use the tangent ratio because we have the opposite and
adjacent sides of the given angle
∴ tan(38°) =
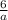
→ Multiply both sides by a to cancel the denominator in the right side
∴ a · tan(38°) = 6
→ Divide both sides by tan(38°) to find a
∴ a =
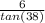
∴ The statement would best represent the value of a is a =