Question

In simplest radical form, what are the solutions to the quadratic equation 0 =3x4x + 5?

Quadratic formula: x= btyb- 4ac

Answer 1

Given:

The quadratic equation is

`0=-3x^2-4x+5`

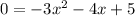
To find:

The simplest radical form of the solution.

Solution:

Quadratic formula:

If a quadratic equation is
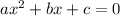`ax^2+bx+c=0`, then

`x=(-b\pm √(b^2-4ac))/(2a)`

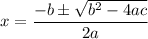
We have,

`0=-3x^2-4x+5`

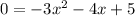
Here, a=-3, b=-4 and c=5. Putting these values in the quadratic formula, we get

`x=(-(-4)\pm √((-4)^2-4(-3)(5)))/(2(-3))`

`x=(4\pm √(16+60))/(-6)`

`x=(4\pm √(76))/(-6)`

`x=(4\pm 2√(19))/(-6)`

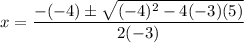
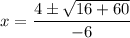
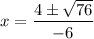
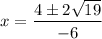
Taking 2 common, we get

`x=(2(2\pm √(19)))/(-6)`

`x=((2\pm √(19)))/(-3)`

`x=-((2\pm √(19)))/(3)`

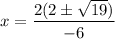
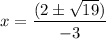
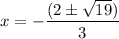
Therefore, the correct option is A.