Answer:
The equation that would be used for the zero product property on will be (x-5)(x-10)=0
Option B is correct.
Explanation:
We need to solve the equation
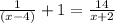
Solving the equation:
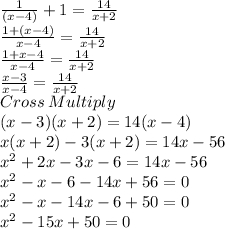
Now, we would factorise to find value of x
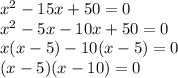
So, the equation that would be used for the zero product property on will be (x-5)(x-10)=0
Option B is correct.