Answer:
The solution to the system of equations be:
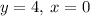
As the consistent system of equations has only one solution, it is independent.
Explanation:
Given the system of equations
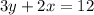
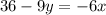
solving the system of equations

Arrange equation variables for elimination
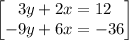
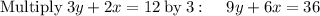
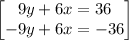
so
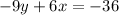

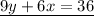
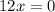

solve 12x=0 for x
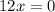
Divide both sides by 12
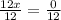

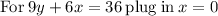
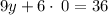

Divide both sides by 9
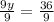
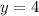
Thus, the solution to the system of equations be:
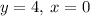
As the consistent system of equations has only one solution, it is independent.