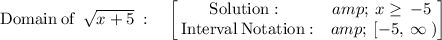Answer:
The domain of the function is:
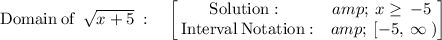
Explanation:
Given the function
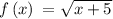
We know that the domain of a function is the set of input or argument values for which the function is real and defined.
From the function, it is clear that for the values x<-5, the function becomes undefined.
For example, for x=-6
√x+5 = √-6+5 = √-1 which is undefined
and for x=-5
√x+5 = √5+5 = √0 which is defined
Thus, the domain of the function is: