Answer:
a) The equation of line perpendicular to above line and passes through point (-7,-4) is
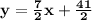
b) The equation of line parallel to above line and passes through point (-7,-4) is

Explanation:
We are given the line:
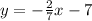
The slope of the above equation is:
 (By comparing with general form
(By comparing with general form
 where m is slope)
where m is slope)
a) Find equation of line perpendicular to above line and passes through point (-7,-4)
If two lines are perpendicular there slopes are opposite reciprocal i.e
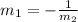
The slope of new line will be:
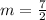
Now finding y-intercept using slope and point (-7,-4)
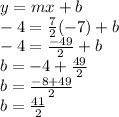
So, the equation of line perpendicular to above line and passes through point (-7,-4) will be:
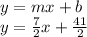
So, the equation of line perpendicular to above line and passes through point (-7,-4) is
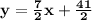
b) Find equation of line parallel to above line and passes through point (-7,-4)
If two lines are parallel there slopes are same i.e

The slope of new line will be:
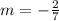
Now finding y-intercept using slope and point (-7,-4)
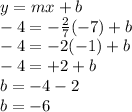
So, the equation of line parallel to above line and passes through point (-7,-4) will be:
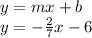
So, the equation of line parallel to above line and passes through point (-7,-4) is
