Question

HELP HELP HELP FAST PLS PLS

Marc sold 500 tickets for the school play. Student tickets cost $2 and adult tickets cost $5. Marc's sales totaled $1,789. a) Write a system of equations that can be used to determine how many of each type of ticket Marc sold b) Solve the system to determine how many adult tickets and how many student tickets Marc sold.

Answer 1

a) System of equations will be:
`x+y=500\: and\:5x+2y=1789`

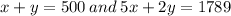
b) Number of adult tickets sold = 263

Number of students tickets sold = 237

Explanation:

Let:

Number of adult tickets sold = x

Number of students tickets sold = y

a)

As Marc sold total 500 tickets, the expression will be:
`x+y=500`

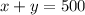
Student tickets cost $2 and adult tickets cost $5. Marc's sales totalled $1,789.

The expression will be:
`5x+2y=1789`

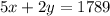
So, system of equations will be:
`x+y=500\: and\:5x+2y=1789`

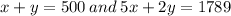
b)

Solve the system to find value of x and y

Let:

`x+y=500--eq(1)\\5x+2y=1789--eq(2)`

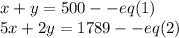
Multiply equation 1 by 2 and subtract

`2x+2y=1000\\5x+2y=1789\\-\:\:\:-\:\:\:\:\:\:\:\:\:-\\------\\-3x=-789\\x=(-789)/(-3)\\x=263`

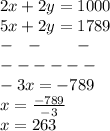
We get value of x = 263

Now finding value of y by putting value of x in eq(1)

`x+y=500\\263+y=500\\y=500-263\\y=237`

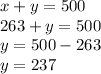
We get value of y = 237

Number of adult tickets sold = x = 263

Number of students tickets sold = y = 237