Answer:
Line 1 and Line 2: Perpendicular
Line 1 and Line 3: Neither
Line 2 and Line 3: Neither
Explanation:
We will write all lines in slope intercept form i.e

where m is slope.
And check
a) If two lines are parallel they have same slope

b) If two lines are perpendicular they have opposite reciprocal slopes i.e
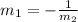
Equation for Line 1:

Already in slope-intercept form
Slope for Line 1 m is:
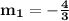
Equation for Line 2:

Converting into slope-intercept form:
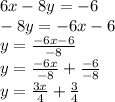
Slope for Line 2 m is:
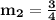
Equation for Line 3:
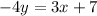
Converting into slope-intercept form:
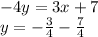
Slope for Line 3 m is:
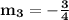
Now, finding answers
Line 1 and Line 2
Checking their slopes:
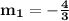 ,
,
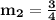
Both lines are perpendicular because they have opposite reciprocal slopes
Line 1 and Line 3
Checking their slopes:
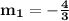 ,
,
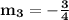
Slopes are neither same, nor opposite reciprocal, so they are neither
Line 2 and Line 3
Checking their slopes:
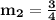 ,
,
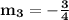
Slopes are neither same, nor opposite reciprocal, so they are neither
The answers are:
Line 1 and Line 2: Perpendicular
Line 1 and Line 3: Neither
Line 2 and Line 3: Neither