Question

Need helpppp i have no idea what to do

Answer 1

Line 1 and Line 2: Perpendicular

Line 1 and Line 3: Neither

Line 2 and Line 3: Neither

Explanation:

We will write all lines in slope intercept form i.e
`y=mx+b`

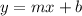
where m is slope.

And check

a) If two lines are parallel they have same slope
`m_1=m_2`

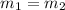
b) If two lines are perpendicular they have opposite reciprocal slopes i.e
`m_1=-(1)/(m_2)`

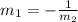
Equation for Line 1:
`y=-(4)/(3)x-4`

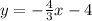
Already in slope-intercept form

Slope for Line 1 m is:
`\mathbf{m_1=-(4)/(3)}`

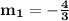
Equation for Line 2:
`6x-8y=-6`

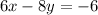
Converting into slope-intercept form:

`6x-8y=-6\\-8y=-6x-6\\y=(-6x-6)/(-8)\\y=(-6x)/(-8)+(-6)/(-8) \\y=(3x)/(4)+(3)/(4)`

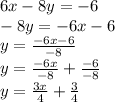
Slope for Line 2 m is:
`\mathbf{m_2=(3)/(4)}`

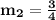
Equation for Line 3:
`-4y=3x+7`

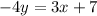
Converting into slope-intercept form:

`-4y=3x+7\\y=-(3)/(4) -(7)/(4)`

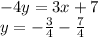
Slope for Line 3 m is:
`\mathbf{m_3=-(3)/(4)}`

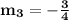
Now, finding answers

Line 1 and Line 2

Checking their slopes:
`\mathbf{m_1=-(4)/(3)}`,
`\mathbf{m_2=(3)/(4)}`

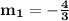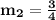
Both lines are perpendicular because they have opposite reciprocal slopes

Line 1 and Line 3

Checking their slopes:
`\mathbf{m_1=-(4)/(3)}`,
`\mathbf{m_3=-(3)/(4)}`

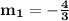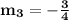
Slopes are neither same, nor opposite reciprocal, so they are neither

Line 2 and Line 3

Checking their slopes:
`\mathbf{m_2=(3)/(4)}`,
`\mathbf{m_3=-(3)/(4)}`

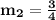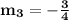
Slopes are neither same, nor opposite reciprocal, so they are neither

The answers are:

Line 1 and Line 2: Perpendicular

Line 1 and Line 3: Neither

Line 2 and Line 3: Neither