Question

Find the distance between w=1+2i and z=3-i

Answer 1

The distance between w=1+2i and z=3-i is 3.61

Explanation:

We need to find the distance between w=1+2i and z=3-i

The formula used is:
`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

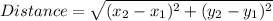
We have
`x_1=1, y_1=2, x_2=3, y_2=1`

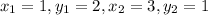
We will use only real numbers and not i for calculating distance.

Putting values and finding distance

`Distance=√((x_1-x_2)^2+(y_1-y_2)^2)\\Distance=√((1-3)^2+(-1-2)^2) \\Distance=√((-2)^2+(-3)^2) \\Distance=√(4+9) \\Distance=√(13)\\Distance=3.61`

So, The distance between w=1+2i and z=3-i is 3.61