Question

Find volumeof right circular cone having base radius 14cm and slant height 14.8cm.​

Answer 1

The cone has a volume of approximately 982.5 cubic centimetres.

* That answer sounds off to me, but I'm not sure. You might want to run through the logic yourself and see if you get the same results.

Explanation:

The volume of a cone is one third that of a cylinder with the same height and base radius. In other words:

`v = \pi r^(2) (h)/(3)`

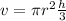
But before using that, we need to know the value of h, height. What we are instead given is the slant height, or the length from tip to edge.

We can use that slant height along with the base radius to get the cone height, as the three of them are the edges of a right triangle, with slant height being the hypotenuse.

To get the height then we can say

`h = \sqrt{s^(2) - r^(2)}`

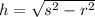
Where h is height, s is slant, and r is radius.

`h = \sqrt{14.8^(2) - 14^(2) }`

`h = √(219.04 - 196)`

`h = √(23.04)`

`h = 4.8`

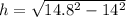
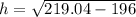
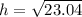
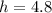
A very squat cone indeed.

Now we can plug that and the radius into the actual cone equation:

`v = \pi (14cm)^(2) (4.8cm)/(3)\\= \pi 196cm^2 * 1.6cm\\\approx 985.2 cm^3`