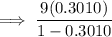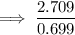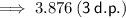Question

Giving my all points away! What is the Value of log5512, when log 2 = 0.3010 and log 3 = 0.4771?

Answer 1

`\\ \rm\Rrightarrow log_5512`

`\\ \rm\Rrightarrow log_52^9`

`\\ \rm\Rrightarrow 9log_52`

• Use change of base

`\\ \rm\Rrightarrow 9(log2)/(log5)`

`\\ \rm\Rrightarrow 3.876`

If your question is something different let me know by which I can change my answer

Answer 2

3.876 (3 d.p.)

Explanation:

Given:

• 
  `\log_(10)2=0.3010`

• 
  `\log_(10)3=0.4771`

Please note: The question gives two values of log base 10 which should be used to help find the value of
`\log_5512`

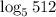
Log Law: Change of Base

`\log_ba=(\log_xa)/(\log_xb)`

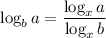
Change the given expression to log base 10:

`\implies \log_5512=(\log_(10)512)/(\log_(10)5)`

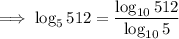
Replace 512 with 2⁹, and 5 with 10/2:

`\implies (log_10(2^9))/(\log_(10)(10)/(2))`

`\textsf{Apply the Power Log law}: \quad \log_ax^n=n\log_ax`

`\implies (9log_10(2))/(\log_(10)(10)/(2))`

`\textsf{Apply the Log Quotient law}: \quad \log_a(x)/(y)=\log_ax - \log_ay`

`\implies (9log_10(2))/(\log_(10)10-\log_(10)2)`

`\textsf{Apply log law}: \quad \log_aa=1`

`\implies (9log_10(2))/(1-\log_(10)2)`

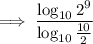
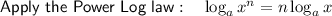
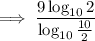
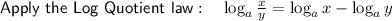
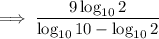
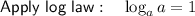
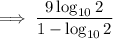
Given:

• 
  `\log_(10)2=0.3010`

Substitute this into the expression and simplify:

`\implies (9(0.3010))/(1-0.3010)`

`\implies (2.709)/(0.699)`

`\implies 3.876\:(\sf 3\: d.p.)`