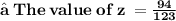- 6x - 2y + z = -2 .......... (i)
- 2x + 3y – 3z = 11 ...........(ii)
- х + 6у = 31 ..............(iii)
After Multiplying 3 with the eq. (i) we will add this to eq. (ii)
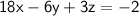

_______________________
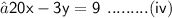
After Multiplying 2 with the eq. (iv) we will add this to eq. (iii)
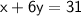
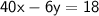
_________________
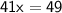
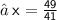
After putting the value of x in the eq. (iii)
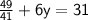
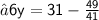
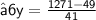
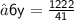
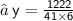
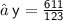
After putting the value of x and y into eq. (i)
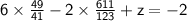
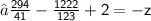
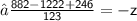
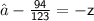
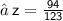
Hence,
![\bf • \: The \: value \: of \: x = (49)/(41) </strong></p><p><strong>[tex] \bf • \: The \: value \: of \: x = (49)/(41)](https://img.qammunity.org/2021/formulas/mathematics/high-school/qlxcdyzg8373xzgnjj3sqn0j47afehi8p6.png)
![\bf • \: The \: value \: of \: y = (611)/(123)</strong></p><p><strong>[tex] \bf • \: The \: value \: of \: y = (611)/(123)](https://img.qammunity.org/2021/formulas/mathematics/high-school/6w0ttkz3je8mvw1lmodev1se8x6p6l2gol.png)