Answer:
center (0, 3) and radius 2√2
Explanation:
Equation of a circle

where:
- (a, b) is the center
- r is the radius
Given equation:
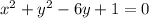
Subtract 1 from both sides:

To create a trinomial with variable y, add the square of half the coefficient of the y term to both sides:
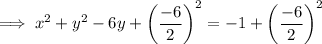
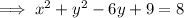
Factor the trinomial with variable y:
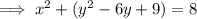
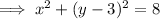
Factor
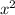 to match the general form for the equation of a circle:
to match the general form for the equation of a circle:
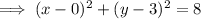
Compare with the general form of the equation for a circle:
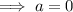

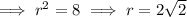
Therefore, the center is (0, 3) and the radius is 2√2