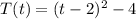Answer:
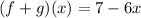 --- (1)
--- (1)
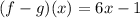 -- (2)
-- (2)
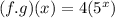 ---- (3)
---- (3)
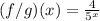 ----- (4)
----- (4)
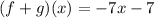 --- (5)
--- (5)
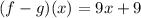 --- (6)
--- (6)
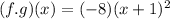 --- (7)
--- (7)
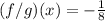 ----- (8)
----- (8)
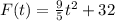 ---- (9)
---- (9)
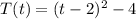 --- (10)
--- (10)
Explanation:
Given
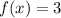
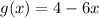
Solving (1): (f + g)(x)
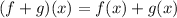
So, we have:
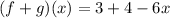
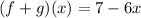
Solving (2): (f - g)(x)
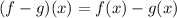
So, we have:
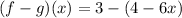
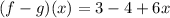
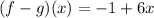
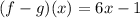
Given
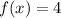

Solving (3): (f . g)(x)

So, we have:
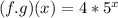
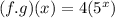
Solving (4): (f / g)(x)
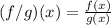
So, we have:
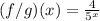
Given
f(x) = x + 1
g(x) = -8 - 8x
Solving (5): (f + g)(x)
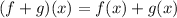
So, we have:
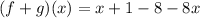
Collect Like Terms
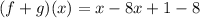
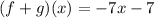
Solving (6): (f - g)(x)
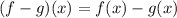
So, we have:
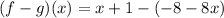
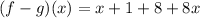
Collect Like Terms
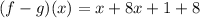
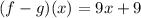
Solving (7): (f . g)(x)
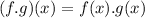
So, we have:
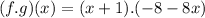
Factorize
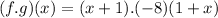
Rewrite as:
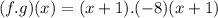
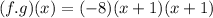
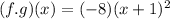
Solving (8): (f / g)(x)
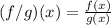
So, we have:

Factorize
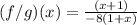
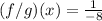
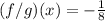
Solving (9):
From the question, we have that:
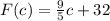

Required
Determine function F in terms of c
The implication of this question is to solve for

If
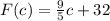 and
and
 ,
,
Then
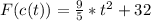
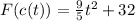
This can be rewritten as:
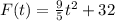
Solving (10):
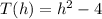
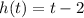
Required
Find

If
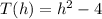 and
and
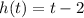 , then
, then

This is gotten by substituting t -2 for h
The solution can be rewritten as: