Answer:
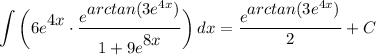
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/bz16ipe6p14y3f6abzxt2zy0j41tg530u9.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/ljowxevzhh8dk8mfdheam579ywk5jvteyi.png)
Integration
- Integrals
- [Indefinite Integrals] Integration Constant C
Integration Property [Multiplied Constant]:
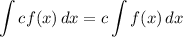
U-Substitution
Explanation:
Step 1: Define
Identify
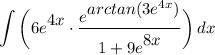
Step 2: Integrate Pt. 1
- [Integrand] Rewrite:
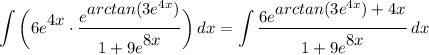
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
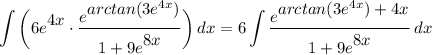
Step 3: integrate Pt. 2
Set variables for u-substitution.
- Set u:
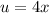
- [u] Differentiate [Basic Power Rule, Multiplied Constant]:
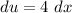
Step 4: Integrate Pt. 3
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
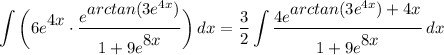
- [Integral] U-Substitution:
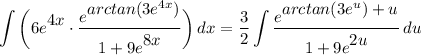
Step 5: Integrate Pt. 4
Set variables for u-substitution #2.
- Set v:
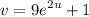
- [v] Differentiate [Exponential Differentiation, Chain Rule]:
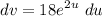
- [v] U-Solve:
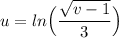
- [dv] U-Solve:
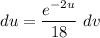
- [U-Solve] Rewrite u:
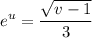
Step 6: Integrate Pt. 5
- [Integral] U-Solve:
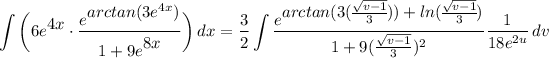
- [Integral] Simplify:
![\displaystyle \int {\bigg( 6e^\big{4x} \cdot \frac{e^\big{arctan(3e^(4x))}}{1 + 9e^\big{8x}} \bigg)} \, dx = (3)/(2)\int {\frac{√(v - 1)e^\big{arctan(√(v - 1))}}{3[1 + v - 1]} (1)/(18((√(v - 1))/(3))^2)\, dv](https://img.qammunity.org/2021/formulas/mathematics/college/wn3pgmiaom824j9fw7w40wv4hgbblwdd1e.png)
- [Integral] Simplify:
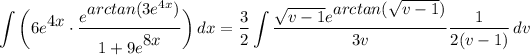
- [Integral] Simplify:
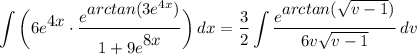
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
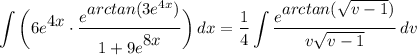
Step 7: Integrate Pt. 6
Set variables for u-substitution #3.
- Set z:
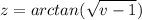
- [z] Differentiate [Arctrig Differentiation, Chain Rule]:
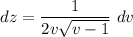
See attachment for rest of work (would not fit entire answer in answering box).