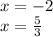Answer:
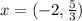
Explanation:
1) We will use the matrix method to solve this problem.
![\left[\begin{array}{ccc}-2/3&1&3\\1&0&-2\\\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/6g46y06w4fkmakygesdh76eyk9ydogoi1b.png)
2) Swap Row₁ and Row₂ to make row reduction easier.
![\left[\begin{array}{ccc}1&0&-2\\-2/3&1&3\\\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/qb14bqvewhof7h06jknvzeoiyxcn7v1ddy.png)
3) Apply to Row₂ : Row₂ +
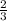 Row₁.
Row₁.
![\left[\begin{array}{ccc}1&0&-2\\0&1&5/3\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/u5erfzdfdpuwf9utscoudzf6hkwe9n4qs5.png)
4) Simplify rows.
![\left[\begin{array}{ccc}1&0&-2\\0&1&5/3\\\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/16bzxkyie8a75ree5d5okn86t0mh9c2bgb.png)
Note: The matrix is now in row echelon form.
The steps below are for back substitution.
5) Apply Row₁ : Row₁ - 0 Row₂.
![\left[\begin{array}{ccc}1&0&-2\0\\0&1&5/3\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/9yp2agj7692llljvj0s4m0y5gaoc824ur3.png)
6) Simplify rows.
![\left[\begin{array}{ccc}1&0&-2\\0&1&5/3\\\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/16bzxkyie8a75ree5d5okn86t0mh9c2bgb.png)
Note: The matrix is now in reduced row echelon form.
7) Therefore,