Question

Students were asked to prove the identity (sec x)(csc x) = cot x + tan x. ​

Answer 1

Let's prove that (sec x)(csc x) is equal to cot x + tan x

`\Longrightarrow \sf (sec(x) )(csc(x))`

`\Longrightarrow \sf (1)/(\cos \left(x\right)\sin \left(x\right))`

`\Longrightarrow \sf (\cos ^2\left(x\right)+\sin ^2\left(x\right))/(\cos \left(x\right)\sin \left(x\right))`

`\Longrightarrow \sf (\cos ^2\left(x\right))/(\cos \left(x\right)\sin \left(x\right)) + (\sin ^2\left(x\right))/(\cos \left(x\right)\sin \left(x\right))`

`\Longrightarrow \sf (\cos\left(x\right))/(\sin \left(x\right)) + (\sin \left(x\right))/(\cos \left(x\right))`

`\Longrightarrow \sf cot(x) + tan(x)`

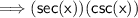
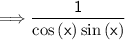
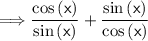
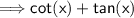
Hence student A did correctly prove the identity properly.

Also Looking at student B's work, he verified the identity properly.

So, Both are correct in their own way.

Part B

Identities used:

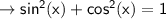`\rightarrow \sf sin^2 (x) + cos^2 (x) = 1` (appeared in step 3)

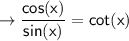`\sf \rightarrow (cos(x) )/(sin(x) ) = cot(x)` (appeared in step 6)

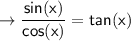`\rightarrow \sf (sin(x ))/(cos(x) ) = tan(x)` (appeared in step 6)