Question

Two brothers, Michael and Alan, were in a bowling league that met once a

week. From past experiences, it is known that both brothers' scores are
approximately normally distributed where Michael has a mean score of 150
with a standard deviation of 30, and Alan has a mean score of 165 with a
standard deviation of 15. Assuming that their scores are independent, which
of the following values is closest to the probability that Michael will have a
greater core than Alan in a single game?
0.16
0.28
0.31
0.33
0.37

Answer 1

The correct option is;

0.28

Explanation:

The given parameters are;

The mean score for Michael,
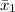`\bar x _1` = 150

The standard deviation, σ₁ = 30

The mean score for Alan,
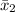`\bar x _2` = 165

The standard deviation, σ₂ = 15

Taking n₁ = n₂ = 1

`z=\frac{(\bar{x}_(1)-\bar{x}_(2))-(\mu_(1)-\mu _(2) )}{\sqrt{(\sigma_(1)^(2) )/(n_(1))-(\sigma _(2)^(2))/(n_(2))}}`

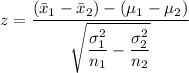
Taking μ₁ - μ₂ = 0

`z=\frac{(150-165)}{\sqrt{(30^(2) )/(1)-(15^(2))/(1)}} \approx -0.577`

The p-value for a z-score of -0.577 from the z-table is 0.28434

Therefore, the probability that Michael, with mean score,
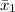`\bar x _1` = 150 will have a greater score than Alan, with a mean score of
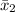`\bar x _2` = 165 is 0.28434 ≈ 0.28

Therefore, the correct option is 0.28