Question

Work out the surface area of a cylinder when the height = 18cm and the volume = 1715cm cubed

Answer 1

We need radius

• πr²h=1715
• πr²(18)=1715
• r²=30.3
• r=5.5cm

Now

LSA

• 2πrh
• 2π(5.5)(18)
• 11(18)(3.14)
• 198(3.14)
• 622.72cm²

Answer 2

813.4 cm² (nearest tenth)

Explanation:

Volume of a cylinder

`\sf V=\pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

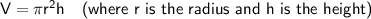
Given:

• h = 18cm
• V = 1715 cm³

Use the Volume of a Cylinder formula and the given values to find the radius of the cylinder:

`\implies \sf 1715=\pi r^2 (18)`

`\implies \sf r^2=(1715)/(18 \pi)`

`\implies \sf r=\sqrt{(1715)/(18 \pi)`

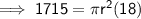
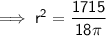
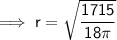
Surface Area of a Cylinder

`\sf SA=2 \pi r^2 + 2 \pi r h \quad\textsf{(where r is the radius and h is the height)}`

Substitute the given value of h and the found value of r into the formula and solve for SA:

`\implies \sf SA=2 \pi \left(\sqrt{(1715)/(18 \pi)\right)^2 + 2 \pi \left(\sqrt{(1715)/(18 \pi)\right)(18)`

`\implies \sf SA=2 \pi \left((1715)/(18 \pi) \right) + 36 \pi \left(\sqrt{(1715)/(18 \pi)\right)`

`\implies \sf SA=(1715)/(9) + 36 \pi \left(\sqrt{(1715)/(18 \pi)\right)`

`\implies \sf SA=813.3908956...`

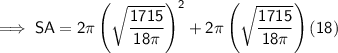
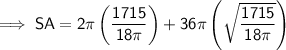
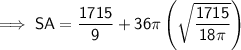
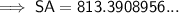
Therefore, the surface area of the cylinder is 813.4 cm² (nearest tenth)