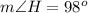Question

Applying the the properties of Congruence.

Quadrilateral GHJK = Quadrilateral LMNP.
Find the given side length or angle measure.

PLEASE HELP NO Scams pleaseeeee !!

Answer 1

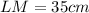`LM = 35cm` and
`m \angle H = 98^o`

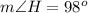
Explanation:

For this problem, it is critical to understand what the opening statement means.

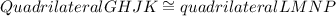`Quadrilateral GHJK \cong quadrilateral LMNP` means that each pair of corresponding sides between shapes are congruent (they have equal length), and each pair of corresponding angles between shapes are congruent (they have equal measure -- or same number of degrees when measured with a protractor).

So, it's important to be able to determine which pairs are the corresponding parts. When the congruence is given like
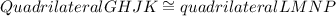`Quadrilateral GHJK \cong quadrilateral LMNP` the letters are in a particular order. That order explains the order in which the shape is drawn out, and they put them in the same order for both shapes to mean that those are the letters that correspond with each other.

So, the first letter of each are a corresponding pair, the second letter of each are a corresponding pair, ... etc

In other words, point G and L correspond, point H and K correspond, etc.

Part 1 -- Find LM

To find the corresponding sides, the sides for these shapes are defined by a two adjacent letters (two letters next to each other in the name, or ... as it wraps around the end of the name... the first and last letter).

`\overline{GH} \cong \overline{LM}\\ \overline{HJ} \cong \overline{MN} \\\overline{JK} \cong \overline{NP}\\\overline{KG} \cong \overline{PL}`

While all of that is true, we only have a few sides with any information in them. Notice that side GH in the first shape, and sides PL & LM in the second shape are the only sides with anything written. So, we just need to determine which sides correspond (and thus, are congruent), so that we know how to move forward. Looking at the list of congruent sides above, we see that
`\overline{GH} \cong \overline{LM}`

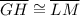
Since the sides (line segments) are congruent, their lengths are equal

`GH = LM`

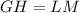
...so we can substitute the expressions for each angle into the equation and solve for the unknown value "x"

`GH = LM\\(4x+3)=(6x-13)`

`(4x+3)+13=(6x-13)+13\\4x+16=6x`

`(4x+16)-4x=(6x)-4x\\16=2x`

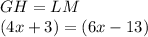
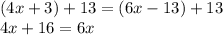
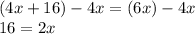
divide both sides by 2

`(16)/(2)=(2x)/(2)\\8=x`

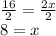
So, to find the length, LM, we just need to look back at the expression for LM:

`LM = 6x-13\\LM = 6(8)-13\\LM = 48-13\\LM = 35`

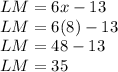
remembering that the lengths are measured in centimeters (as indicated on the diagram):
`LM = 35cm`

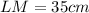
Part 2 -- Find m∠H

To find the corresponding angles, the angles for these shapes are defined by a single letter, so since the points correspond in order, the names of the shapes tell which angles are congruent.

`\angle G \cong \angle L\\\angle H \cong \angle M\\\angle J \cong \angle N\\\angle K \cong \angle P`

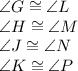
While all of that is true, we only have a few angles with any information in them. Notice that ∠H in the first shape, and ∠L & ∠M in the second shape are the only angles with anything written. So, we just need to determine which angles correspond (and thus, are congruent), so that we know how to move forward. Looking at the list of congruent angles above, we see that

`\angle H \cong \angle M`

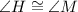
Since the angles are congruent, their measures are equal

`m\angle H = m\angle M`

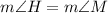
...so we can substitute the expressions for each angle into the equation and solve for the unknown value "y"

`m\angle H = m\angle M\\(9y+17)=(11y-1)`

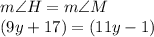
subtract 1 from both sides

`(9y+17)+1=(11y-1)+1\\9y+18=11y`

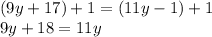
subtract 9y from both sides

`\\(9y+18)-9y=(11y)-9y\\18=2y`

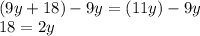
divide both sides by 2

`(18)/(2)=(2y)/(2)\\9=y`

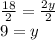
So, to find angle H, we just need to look back at the expression for the measure of angle H:

`m\angle H = 9y+17\\m\angle H = 9(9)+17\\m\angle H = 81+17\\m\angle H = 98`

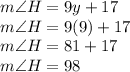
remembering that the angle is measured in degrees (as indicated on the diagram):
`m \angle H = 98^o`