Answer:
813.4 cm² (nearest tenth)
Explanation:
Volume of a cylinder
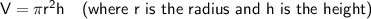
Given:
Use the Volume of a Cylinder formula and the given values to find the radius of the cylinder:
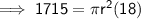
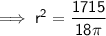
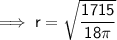
Surface Area of a Cylinder

Substitute the given value of h and the found value of r into the formula and solve for SA:
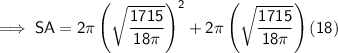
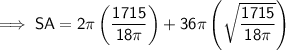
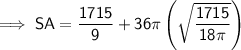
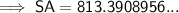
Therefore, the surface area of the cylinder is 813.4 cm² (nearest tenth)