1. The slope between (-1, -3) and (4, 0) is: d. 3/5.
2. The slope of the equation 3y = 15x + 9 is: a. 5.
3. The equation in slope-intercept form is: c. y = -3x + 5.
4. The equation of the line in slope-intercept form is: a. y = 2x + 3.
5. The equation in point-slope form is: c. y – 3 = -3(x – 1).
6. The equation of the function graphed above is: c. y = x - 4.
7. The slope of this function is: d. -3
In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;
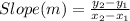
Slope(m) = (0 + 3)/(4 + 1)
Slope(m) = 3/5.
Part 2.
The slope-intercept form of the equation of a straight line refers to the general equation of a linear function and it is represented by this mathematical equation;
y = mx + b
Where:
- m is the slope.
- x and y are the points.
- b is the y-intercept.
By rewriting the equation 3y = 15x + 9 in slope-intercept form, we have;
y = 5x + 19/3
slope (m) = 5.
Part 3.
At data point (1, 2) and a slope of -3, an equation for this line can be calculated by using the point-slope form as follows:
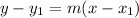
y - 2 = -3(x - 1)
y = -3x + 5
Part 4.
At data point (0, 3) and a slope of 2, an equation for this line can be calculated by using the point-slope form as follows:
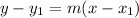
y - 3 = 2(x - 0)
y = 2x + 3
Part 5.
Slope (m) = (12 - 3)/(-2 - 1)
Slope (m) = -3.
At data point (1, 3) and a slope of -3, an equation for this line can be calculated by using the point-slope form as follows:
y - 3 = -3(x - 1).
Part 6.
With an x-intercept (a) of (4, 0) and a y-intercept (b) of (0, -4), an equation for the graph is given by;
x/a + y/b = 1
x/4 - y/4 = 1
x - y = 4
y = x - 4
Part 7.
Based on the table of vaues, the slope is as follows;
Slope(m) = (0 - 3)/(1 - 0)
Slope(m) = -3.