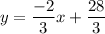Answer:
Explanation:
Equation of the line in slope- intercept form:
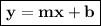
Here, m is the slope and b is the y-intercept
Find the slope with the given two points.
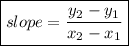
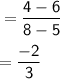
Slope = -2/3 and choose any one the given points.
Substitute m = -2/3 and (5,6) in the above equation and find 'b'
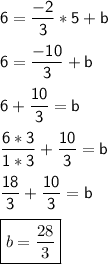
Equation of the line: