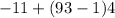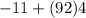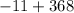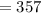Answer:
357
Explanation:
Arithmetic sequence is a sequence where the successive terms have a common difference for example
1,2,3,4,5..... is a arithmetic sequence because they have a common difference of one..
Use the arithmetic sequence formula for nth terms.
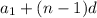
Where en is the nth term you trying to find, a1 is the first term of the series and d is the common difference.
a1 is 11, n is 93 and d is 4 so we get