Answer:
The rectangle has a width of 18 inches and a height length of 8 inches.
Explanation:
The perimeter of a rectangle is described by the equation:
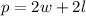
where l is width, h is height, and p is perimeter.
We're also told that the total perimeter is 52 inches.
We're also told that the length is six inches less than three times the width. We can express that as
 .
.
We can plug that definition of w into the perimeter equation to find the length:
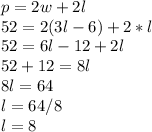
Now we can take that and the given perimeter, and substitute those into the perimeter equation to find the width:
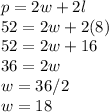
So the width is 18