Question

The local water supply has a leak, it is losing 4 gallons of water every second.

After 15 seconds, the water level is at 1024 gallons. Write an equation to
represent the situation: *

Answer 1

An equation to represent the situation would be:

• 
  `y = 4x + 964`

Explanation:

Given that the water supply is losing 4 gallons of water every second.

It means the rate of change = 4 gallons per second

• Given that after 15 seconds, the water level is at 1024 gallons.

So the equation becomes

1024 = 4(15) + b

comparing with the slope-intercept form of the equation of a line

`y = mx+b`

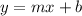
where m is the slope (rate of change) and b is the y-intercept

so

`1024 = 4(15) + b`

`1024 = 60 + b`

`1024 - 60 = b`

`b = 964`

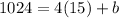
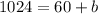
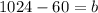
So, the value of y-intercept i.e b=964

Thus, the equation will be

`y = mx+b`

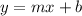
substituting the value rate of change i.e m = 4 and b=964

`y = 4x + 964`

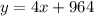
Therefore, an equation to represent the situation would be:

• 
  `y = 4x + 964`