Answer:
Length of RT = 6 mm
Explanation:
When the triangles are similar the ratio of corresponding sides are equal.
In given triangles we have ( we can take ratio of two sides also)

We need to find length of RT = x
While length of JI= 8 mm
Length of HI = 12 mm
Length of SR = 9 mm
Putting values in formula and finding length of RT
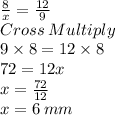
So, Length of RT = x = 6 mm