Answer:
Angle 1= 54°
Angle 2= 144°
Angle 3 = 126°
Angle 4 = 36°
Explanation:
We are given measures of the angles of a quadrilateral are 3:8:7:2
Let the common ratio = x
The angles will be:
Angle 1= 3x,
Angle 2= 8x,
Angle 3 =7x
Angle 4 =2x
We know that sum of all angles of quadrilateral = 360°
We can write as:
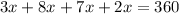
Solving to find x,
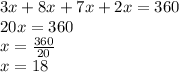
We get value of x = 18
Now, finding angles:
Angle 1= 3x = 3(18) = 54°
Angle 2= 8x = 8(18) = 144°
Angle 3 =7x = 7(18) = 126°
Angle 4 =2x = 2(18) = 36°