Question

Which is the length of the hypotenuse for a right triangle with leg a = 8 and leg b = 15 cm?

Answer 1

`\huge{ \boxed{ \tt{17 \: cm}}}`

Option D is the correct choice.

☪ First , Let's know about right triangle , legs and hypotenuse :

• A right triangle is a triangle with an angle of 90°.
• The two sides that form the right angle are called legs.
• The opposite side of right angle is the hypotenuse.

☥ Let's explore about The Pythagorean Theorem :

• Pythagoras was one of the first mathematician to recognize the relationship between the sides of a right triangle. This special relationship forms ' The Pythagorean Theorem '.
• The Pythagorean theorem states that the sum of the squares of the legs of a right triangle equals the square of the length of a hypotenuse.
• In algebraic terms , The Pythagorean Theorem is stated as :
  `\boxed{ \sf{ {a}^(2) + {b}^(2) = {c}^(2) }}`

------------------------------------------------------------

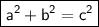
☯ Now , let's start to solve :

✑
`\underline{ \underline{ \text{Given}}} :`

• a = 8 cm , b = 15 cm

✑
`\underline{ \underline{ \text{To\: Find}}} :`

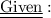
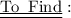
• Length of a hypotenuse ( c )

✐
`\underline{ \bold{ \underline{Using \: Pythagorean \: Theorem}}} \: :`

☞
`\boxed{ \bold{ \sf{ {a}^(2) + {b}^(2) = {c}^(2) }}}`

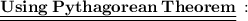
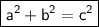
Substitute the known values :

↦
`\sf{ {8}^(2) + {15}^(2) = {c}^(2)}`

↦
`\sf{64 + 225 = {c}^(2) }`

↦
`\sf{289 = {c}^(2) }`

↦
`\sf{ {c}^(2) = 289 }`

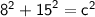
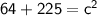
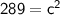
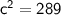
Take the square roots of both sides :

↦
`\sf{ \sqrt{ {c}^(2) } = √(289)}`

↦
`\boxed{ \sf{c = 17 \: cm}}`

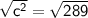
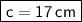
The length of the hypotenuse is
`\boxed{ \bold{ \text{17 \: cm}}}`.

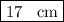And we're done!!

Hope I helped!

Have a wonderful day ! ツ

~TheAnimeGirl ♡

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁