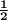Identify the k-value that makes the relationship shown in the table below proportional.

Question

asked Jun 20, 2021 104k views

1 Answer

Ayush Surana · Answer 1 · 2021-06-24T20:39:04+0000

Answer:

The value of k that makes the relationship shown in the table below proportional is
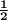
$\mathbf{(1)/(2)}$

Explanation:

The relation is proportional if
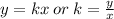
$y=kx \:or\:k=(y)/(x)$

Putting values of x and y to find k.

For x =2 and y =1 k is:
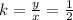
k=(y)/(x)=(1)/(2)

For x =4 and y =2 k is:
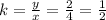
k=(y)/(x)=(2)/(4) =(1)/(2)

For x =6 and y = 3 k is:
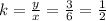
k=(y)/(x)=(3)/(6) =(1)/(2)

For x = 8 and y = 4 k is:
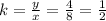
k=(y)/(x)=(4)/(8) =(1)/(2)

For x =10 and y = 5 k is:
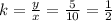
k=(y)/(x)=(5)/(10) =(1)/(2)

So, The value of k that makes the relationship shown in the table below proportional is
$\mathbf{(1)/(2)}$