Question

X^4-13x^2+12=0 solve for x

Answer 1

x = ± 1, x = ± 2
`√(3)`

Explanation:

Given

`x^(4)` - 13x² + 12 = 0

Use the substitution u = x² , then

u² - 13u + 12 = 0 ← in standard form

(u - 1)(u - 12) = 0 ← in factored form

Equate each factor to zero and solve for u

u - 1 = 0 ⇒ u = 1

u - 12 = 0 ⇒ u = 12

Now substitute x² = u back, that is

x² = 1 ( take the square root of both sides )

x = ±
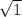`√(1)` = ± 1

x² = 12 , then

x = ±
`√(12)` = ±
`√(4(3))` = ± 2
`√(3)`

Answer 2

`x^4-13x^2+12=0\\`

Let
`x^2=x`

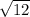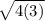`x^2-13x+12=0\\(x-12)(x-1)=0\\x=1,12\\x^2=1,12\\x=1,-1,√(12),-√(12)`