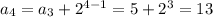Question

What is the recursive of this:

Answer 1

`a_n=a_(n-1)+2^(n-1)\ \ n>1`

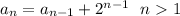
Explanation:

Recursive Sequence

We are given the following sequence:

-1, 1, 5, 13...

It's required to find the recursive term for the sequence.

A recursive formula calculates each term as a function of one or more previous terms.

To find the recursive formula, we must find a pattern and transform it into a math expression.

Let's write the sequence, and below it, the difference of consecutive terms:

-1, 1, 5, 13...

+2, +4, +8

Note the difference between consecutive terms is always a power of 2, starting from 2^1, 2^2, 2^3.

The exponent is one less than the number of the term, thus:

`a_n-a_(n-1)=2^(n-1)`

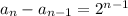
Thus:

`\mathbf{a_n=a_(n-1)+2^(n-1)\ \ n>1}`

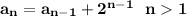
Testing:

n=1

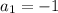`a_1=-1` (given).

n=2

`a_2=a_(1)+2^(2-1)=-1+2^(1)=1`

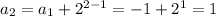
n=3

`a_3=a_(2)+2^(3-1)=1+2^(2)=5`

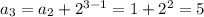
n=4

`a_4=a_(3)+2^(4-1)=5+2^(3)=13`