Question

Find the value of n so that the following points will lie on a line. (3,5), (−1,3), and (7,n)

Answer 1

We get value of n=7

Explanation:

If points lie on same line, they have same slope.

First we will find slope of points (3,5), (−1,3)

Using formula:
`Slope=(y_2-y_1)/(x_2-x_1)`

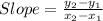
We have
`x_1=3, y_1=5, x_2=-1, y_2=3`

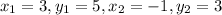
Finding slope

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(3-5)/(-1-3) \\Slope=(-2)/(-4) \\Slope=(1)/(2)`

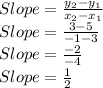
Using slope 1/2 and points (−1,3), and (7,n) we can find value of n

`Slope=(y_2-y_1)/(x_2-x_1)\\(1)/(2) =(n-3)/(7-(-1)) \\(1)/(2) =(n-3)/(7+1) \\(1)/(2) =(n-3)/(8)\\Cross\:Multiply\\1(8)=2(n-3)\\8=2n-6\\2n=8+6\\2n=14\\n=(14)/(2)\\n=7`

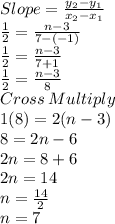
So, we get value of n=7