Answer:
Width of rectangle = 6 m
Length of rectangle = 11 m
Explanation:
Let width of rectangle = w
Length of rectangle = 3w-7
Area of rectangle = 66 m²
We need to find length and width of rectangle
The formula used is:
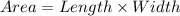
Putting values and finding w
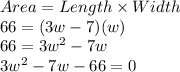
Solve using quadratic formula:
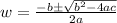
We have a=3, b=-7, c=-66
Putting values and finding w
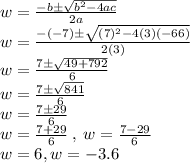
We get values of w as w=6 and w=-3.6
As we know width cannot be negative, so considering w = 6
So, Width = 6
Length = 3w-7 = 3(6)-7 = 18-7 = 11
So, Width of rectangle = 6 m
Length of rectangle = 11 m