Question

Circle Y is shown. Chords R T and S U intersect. Arc R S is 106 degrees. The angle that intercepts arc R S is 94 degrees.

In circle Y, what is mArc T U?

82°
100°
106°
118°

Answer 1

b. 82˚

Explanation:

Answer 2

Given:

Consider the below figure attached with this question.

In Circle Y, Chords R T and S U intersect.

Arc RS is 106 degrees.

The angle that intercepts arc RS is 94 degrees.

To find:

The measure of arc(TU).

Solution:

If two chords intersect each other insider the circle, then the half of sum of intercepted arcs is equal to the angle on intersection of those arcs.

For the given problem,

`(1)/(2)[m(arc RS)+m(arc TU)]=94^\circ`

`(1)/(2)[106^\circ+m(arc TU)]=94^\circ`

`106^\circ+m(arc TU)=2* 94^\circ`

`106^\circ+m(arc TU)=188^\circ`

`m(arc TU)=188^\circ-106^\circ`

`m(arc TU)=82^\circ`

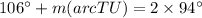
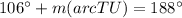
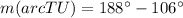
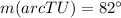
The measure of arc(TU) is 82 degrees.

Therefore, the correct option is A.