Question

4. y=-x(squared) -8x - 16
Axis of Symmetry:
Vertex:
Domain:
Range:

Answer 1

Hey! You can actually look up online a calculator for this. You can type in your equation and they will both graph your equation and answer these questions for you without you having to do any work. And it’s much faster! Good luck ❤️

Answer 2

`y = - {x}^(2) - 8x - 16`

`(d)/(dx) ( - {x}^(2) - 8x - 16) \\ - 2x - 8 = 0 \\ - 2x = 8 \\ x = - 4`

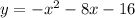
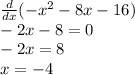
Axis of Symmetry is x = h. Therefore the axis of symmetry is x = -4

`y = - ( - {4})^(2) - 8( - 4) - 16 \\ y = - 16 + 32 - 16 \\ y = 0`

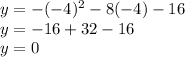
The vertex is at (h, k). Therefore the vertex is at (-4,0)

Domain for Quadratic Function is all set of real number.

Range is from minimun value to maximum value. However, downward parabola doesn't have minimum value. Therefore the range is less or equal than the vertex for k value.

The range is y<= 0