Answer:
339
Explanation:
Exponential Function
General form of an exponential function:

where:
- a is the initial value (y-intercept)
- b is the base (growth/decay factor) in decimal form
- x is the independent variable
- y is the dependent variable
If b > 1 then it is an increasing function
If 0 < b < 1 then it is a decreasing function
Given information:
- a = 240 (initial population of bacteria)
- x = time (in hours)
- y = population of bacteria
Therefore:
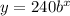
To find an expression for the population after 1 hour, substitute x = 1 into the found equation:
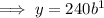
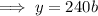
We are told that the population after 9 hours is double the population after 1 hour. Therefore, make y equal to twice the found expression for the population after 1 hour, let x = 9, then solve for b:
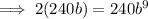
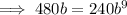
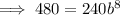
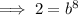
![\implies b=\sqrt[8]{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dhi14bns2o8qkpynkit39enn9wsbc29jq8.png)
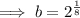
Therefore, the final exponential equation modelling the given scenario is:
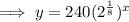

To find how many bacteria there will be after 4 hours, substitute x = 4 into the found equation:
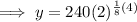
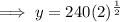

Therefore, there will be 339 bacteria (rounded to the nearest whole number) after 4 hours.