Question

Triangle A C D is shown. A line is drawn from point D to point B on side A C to form a right angle. Line A D is labeled s. The length of A B is 8, the length of B C is 5, and the length of B D is 15.

What is the value of s in units?

Answer 1

17

Explanation:

Answer 2

s = 17units

Explanation:

For this problem, we are trying to find a specific unknown side length.

We're actually given some extraneous information (information that is not needed to solve the problem): It isn't necessary to know that BC is 5.

If the side AD with the unknown length is part of a right triangle (the triangle in red in the attached diagram), we can use the Pythagorean Theorem to solve for AD.

It isn't clear if the diagram you were provided gives ∠ABD as a right angle, if it only gives ∠CBD as a right angle, or if it gives both as a right angle. Below, we prove that it doesn't matter, because regardless, both must be right angles.

Is Triangle ABD a "right triangle"?

Since B is between A and C, then the two angles ∠ABD & ∠CBD form a linear pair, and by the linear pair postulate are supplementary. Since they are supplementary, their measures add to 180°. Using the fact that all right angles are 90°, substitution, the subtraction property of equality, arithmetic, the measure of ∠ABD is also 90°, and thus must be a right angle. Thus, based on the given information, both ∠ABD & ∠CBD must be right angles.

Consequently, triangle ABD is a right triangle, by definition (it is a triangle that has a right angle).

Pythagorean Theorem

Since triangle ABD is a right triangle, the Pythagorean Theorem can be applied.

The Pythagorean Theorem states that
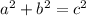`a^(2) +b^(2) =c^(2)` where "c" is the hypotenuse (the side across from the right angle) and "a" and "b" the the lengths of the two other sides (called legs) of the right triangle. (Aside: Because of the commutative property of addition, it doesn't matter which of the two legs' lengths is used for a, and which is used for b. The only thing that is required is that "c" be the length of the hypotenuse)

In our triangle, side AD, with unknown length "s" is the length of our hypotenuse, and sides AB and BD are the two legs. Substituting values into the Pythagorean Theorem equation, we can solve for the unknown "s":

`a^(2) +b^(2) =c^(2)`

`(8)^(2) +(15)^(2) =(s)^(2)`

`64 +225 =s^(2)`

`289 =s^(2)`

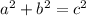
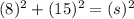
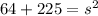
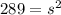
Applying the square root property...

`\pm √(289) =\sqrt{s^(2)}`

`s=17 \text{ or } s=-17`

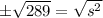
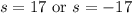
Final Solution

We discard the negative solution we obtained, since s represents the length of the side of a triangle.

s = 17units