Answer:

Explanation:
This is a right triangle and we are looking for a missing side. We can use the Pythagorean Theorem to find x.

where a and b are the legs and c is the hypotenuse.
In this triangle, the legs are 28 and 13 because they make up the right right angle. x is the hypotenuse because it is opposite the right angle.

Substitute the values in.
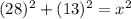
Solve the exponents.
- (28)²=28*28=784
- (13)²=13*13=169
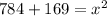
Add the two numbers.
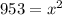
We want to solve for x, which means we must isolate it.
The x is being squared. The inverse of a square is the square root, so take the square root of both sides of the equation.

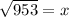
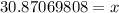
Let's round to the nearest hundredth. The 7 in the thousandth place tells us to round the 8 to a 9.
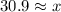
x is about 30.9