Answers:
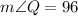

==========================================
Step-by-step explanation:
Check out the diagram below. I've formed triangle PQR such that PQ and QR are congruent sides shown by the tickmarks. This isosceles triangle has congruent base angles, which are opposite the tickmark sides. Those base angles are P and R. Since P is 42 degrees, so is R.
Let x be the measure of angle Q
For any triangle, the three angles always add to 180
P+Q+R = 180
42+x+42 = 180
x+84 = 180
x = 180-84
x = 96
Therefore, angle Q is 96 degrees.