Answer:
$7.55
Explanation:
We can solve this by using a system of equations. The equations would be set up like this:
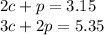
Let's isolate a variable in the first equation:
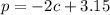
Now we can plug this in to the second equation:

Now that we have found c we can find p by plugging c in to an equation

We have found both variables now we can use the following equation to answer the question:

Therefore, the price in dollars of 4 cucumbers and 3 peppers is $7.55.
I hope this helps!!
- Kay :)