Answer:
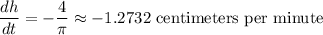
The water level is dropping by approximately 1.27 centimeters per minute.
Explanation:
Please refer to the attached diagram.
The height of the conical container is 6 cm, and its radius is 1 cm.
The container is leaking water at a rate of 1 cubic centimeter per minute.
And we want to find the rate at which the water level h is dropping when the water height is 3 cm.
Since we are relating the water leaked to the height of the water level, we will consider the volume formula for a cone, given by:
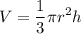
Now, we can establish the relationship between the radius r and the height h. At any given point, we will have two similar triangles as shown below. Therefore, we can write:
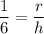
Solving for r yields:
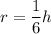
So, we will substitute this into our volume formula. This yields:

Now, we will differentiate both sides with respect to time t. Hence:
![\displaystyle (d)/(dt)[V]=(d)/(dt)\Big[(1)/(108)\pi h^3\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/1rkpiugyxn57pdg8j2n2i2j4t3dnl7c0xk.png)
The left is simply dV/dt. We can move the coefficient from the right:
![\displaystyle (dV)/(dt)=(1)/(108)\pi(d)/(dt)\big[h^3\big]](https://img.qammunity.org/2021/formulas/mathematics/college/cd5gztq1jmzukebbces17q1wikuc61jk8h.png)
Implicitly differentiate:
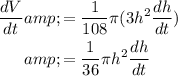
Since the water is leaking at a rate of 1 cubic centimeter per minute, dV/dt=-1.
We want to find the rate at which the water level h is dropping when the height of the water is 3 cm.. So, we want to find dh/dt when h=3.
So, by substitution, we acquire:

Therefore:

Hence:
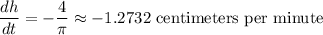
The water level is dropping at a rate of approximately 1.27 centimeters per minute.