Question

Which statement about the graph of the line y=x+1/2 will be true if the 1/2 is replaced by -2

Answer 1

If the
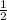`\( (1)/(2) \)` in the equation
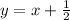`\( y = x + (1)/(2) \)` is replaced by -2, the new equation becomes
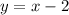`\( y = x - 2 \)`. The statement about the graph that will be true is that the new line will have the same slope as the original line but a different y-intercept.

Explanation:

When replacing
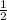`\( (1)/(2) \)` with -2 in the equation
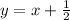`\( y = x + (1)/(2) \)`, we get
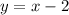`\( y = x - 2 \)`. This transformation changes the y-intercept of the line without affecting its slope. The original equation
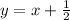`\( y = x + (1)/(2) \)` has a y-intercept of
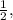`\( (1)/(2) \),` meaning the line crosses the y-axis at the point
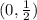`(0, \( (1)/(2) \))`. On the other hand, the new equation
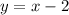`\( y = x - 2 \)` has a y-intercept of -2, so the line crosses the y-axis at the point (0, -2).

The slope of both equations is 1, as indicated by the coefficient of x. Therefore, the lines have the same steepness or inclination. The change in the y-intercept, however, results in a vertical shift of the graph. Visually, the new line will be parallel to the original line but will be shifted downward on the coordinate plane.

This shift doesn't alter the slope, emphasizing that the replacement of
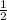`\( (1)/(2) \)` with -2 only affects the position of the line along the y-axis. In summary, the statement about the graph being true means recognizing that the replacement changes the y-intercept while maintaining the original slope.

Answer 2

The y-intercept (where the line hits the y-axis) will move from (0, 1/2) to (0, -2)